Baihe He, Qiang Lu, Qingyun Yang, Jake Luo, and Zhiguang Wang.

Received: 24 March 2022 / Accepted: 14 April 2022.

TaylorGP

The paper Taylor Genetic Programming for Symbolic Regression has been accepted by GECCO-2022 . You could also see our appendix for more details.

1.Abstract

Genetic programming (GP) is a commonly used approach to solve symbolic regression (SR) problems. Compared with the machine learning or deep learning methods that depend on the pre-defined model and the training dataset for solving SR problems, GP is more focused on finding the solution in a search space. Although GP has good performance on large-scale benchmarks, it randomly transforms individuals to search results without taking advantage of the characteristics of the dataset.So, the search process of GP is usually slow, and the final results could be unstable. To guide GP by these characteristics, we propose a new method for SR, called Taylor genetic programming (TaylorGP). TaylorGP leverages a Taylor polynomial to approximate the symbolic equation that fits the dataset. It also utilizes the Taylor polynomial to extract the features of the symbolic equation: low order polynomial discrimination, variable separability, boundary, monotonic, and parity. GP is enhanced by these Taylor polynomial techniques. Experiments are conducted on three kinds of benchmarks: classical SR, machine learning, and physics. The experimental results show that TaylorGP not only has higher accuracy than the nine baseline methods, but also is faster in finding stable results.

2. Code

You could get the code from our github.

Requirements

Make sure you have installed the following python version and pacakges before start running our code:

• python3.6~3.8
• scikit-learn
• numpy
• sympy
• pandas
• time
• copy
• itertools
• timeout_decorator
• scipy
• joblib
• numbers
• itertools
• abc
• warnings
• math

Our experiments were running in Ubuntu 18.04 with Intel(R) Xeon(R) Gold 5218R CPU @ 2.10GHz.

Examples

We provide an example to test whether the module required by Taylor GP is successfully installed:

python TaylorGP.py

In addition, you can run the specified dataset through the following method:

python TaylorGP.py --fileName="Feynman/F24.tsv"

3. Experiments

DataSet

We evaluate the performance of TaylorGP on three kinds of benchmarks: classical Symbolic Regression Benchmarks (SRB), Penn
Machine Learning Benchmarks (PMLB), and Feynman Symbolic Regression Benchmarks (FSRB) .(You could get them from directories GECCO, PMLB and Feynman respectively).The distribution of the total 81 benchmark sizes by samples and features is shown in the following.

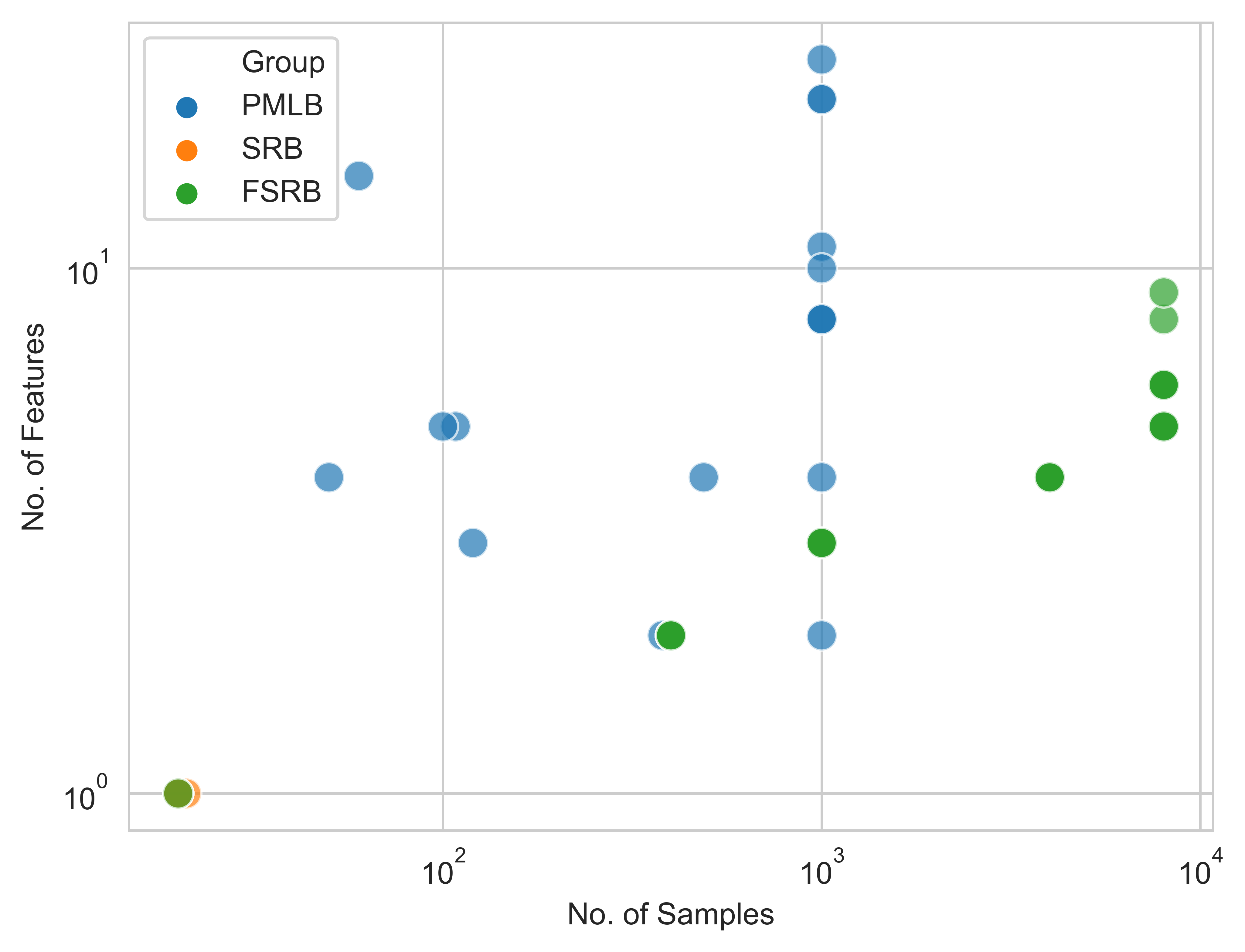
The details of these benchmarks are listed in the appendix.

Performance

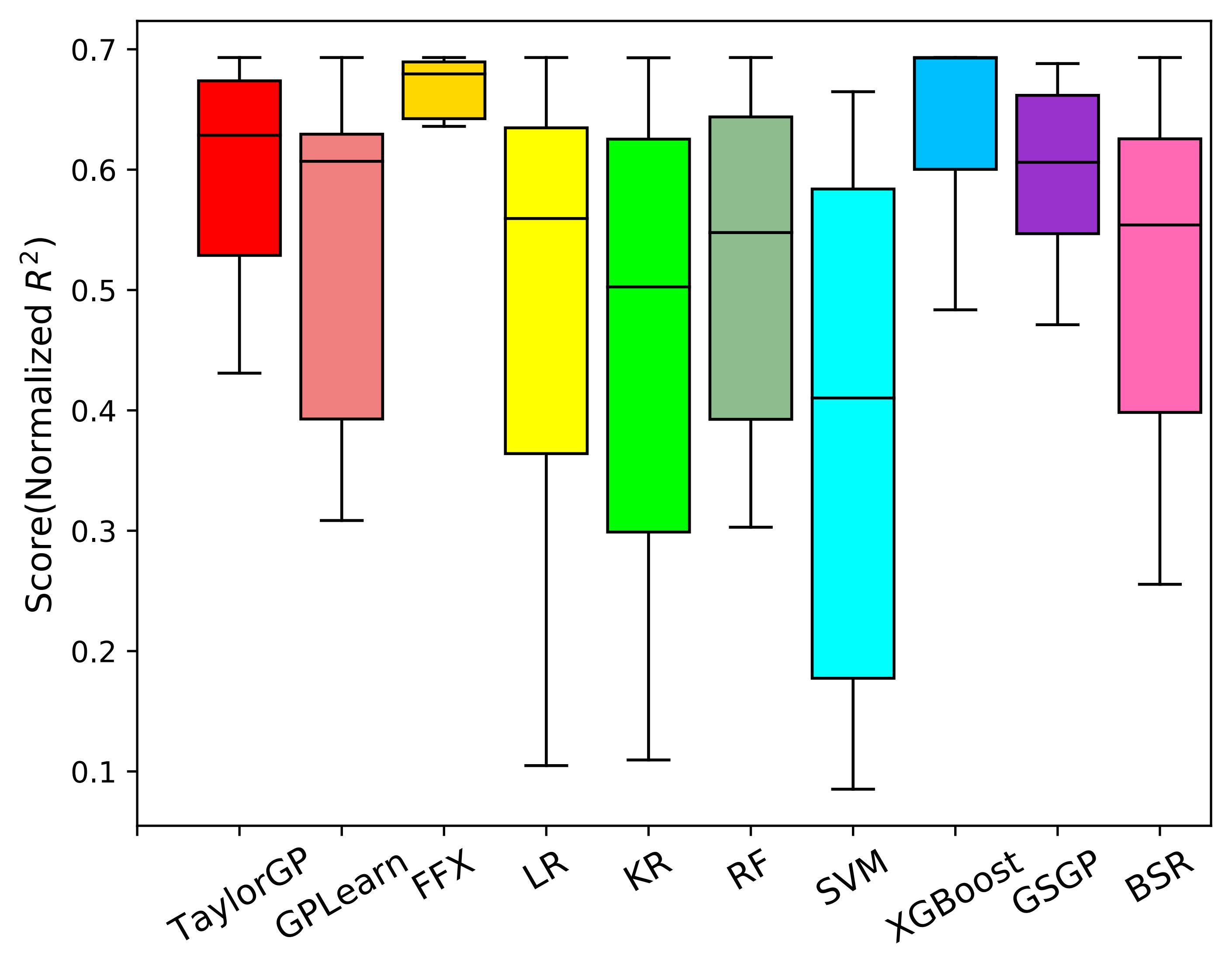
We compare TaylorGP with two kinds of baseline algorithms \footnote{The nine baseline algorithms are implemented in SRBench : four symbolic regression methods and five machine learning methods. The symbolic regression methods include GPlearn, FFX , geometric semantic genetic programming (GSGP) and bayesian symbolic regression (BSR). The machine learning methods include linear regression (LR), kernel ridge regression (KR), random forest regression (RF), support vector machines (SVM), and XGBoost .

As shown in the figure below , we illustrate the normalized R^2 scores of the ten algorithms running 30 times on all benchmarks. Since the normalized R^2 closer to 1 indicates better results, overall TaylorGP can find more accurate results than other algorithms.

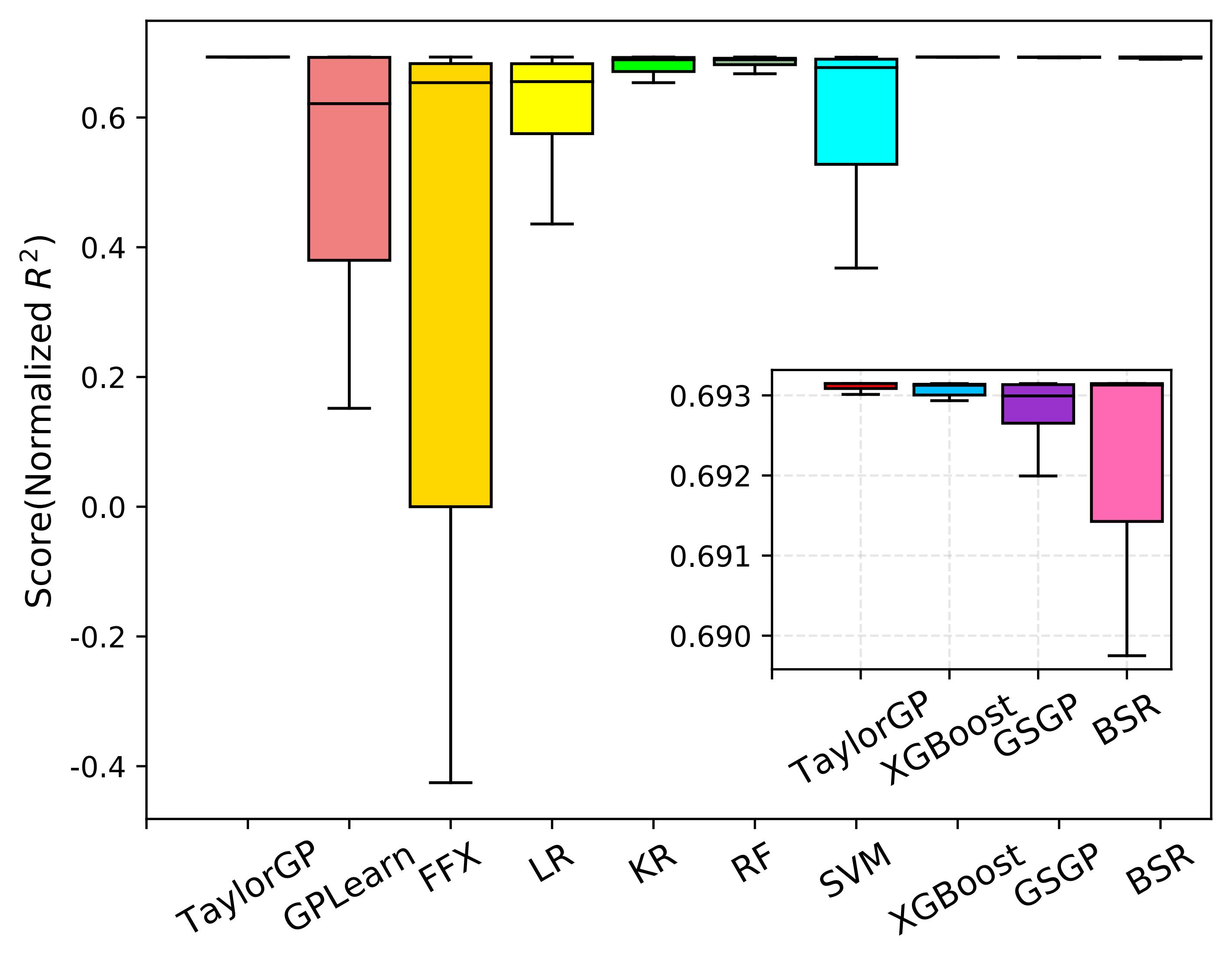
Normalized R^2 comparisons of the ten SR methods on classical Symbolic Regression Benchmarks

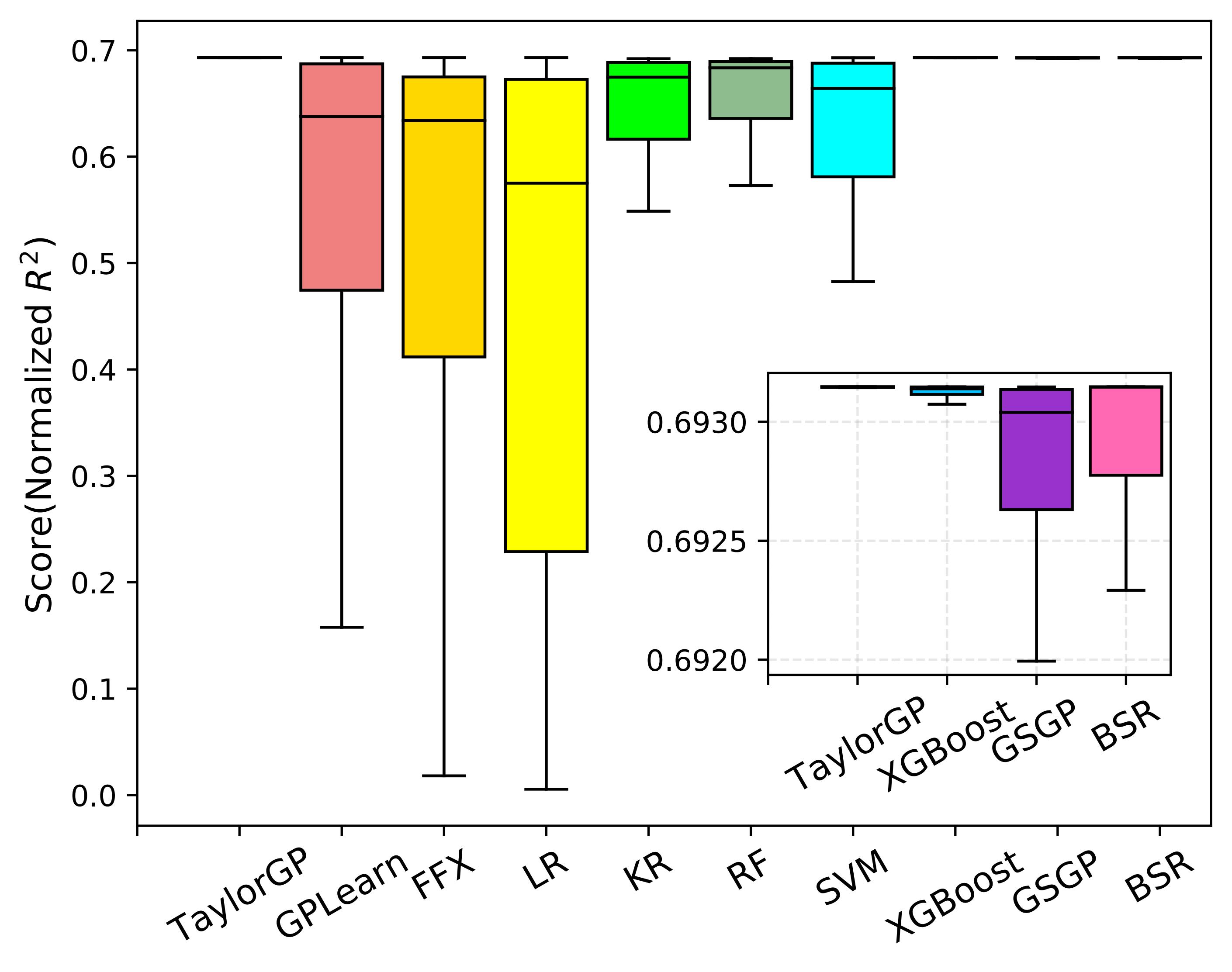
Normalized R^2 comparisons of the ten SR methods on Feynman Symbolic Regression Benchmarks

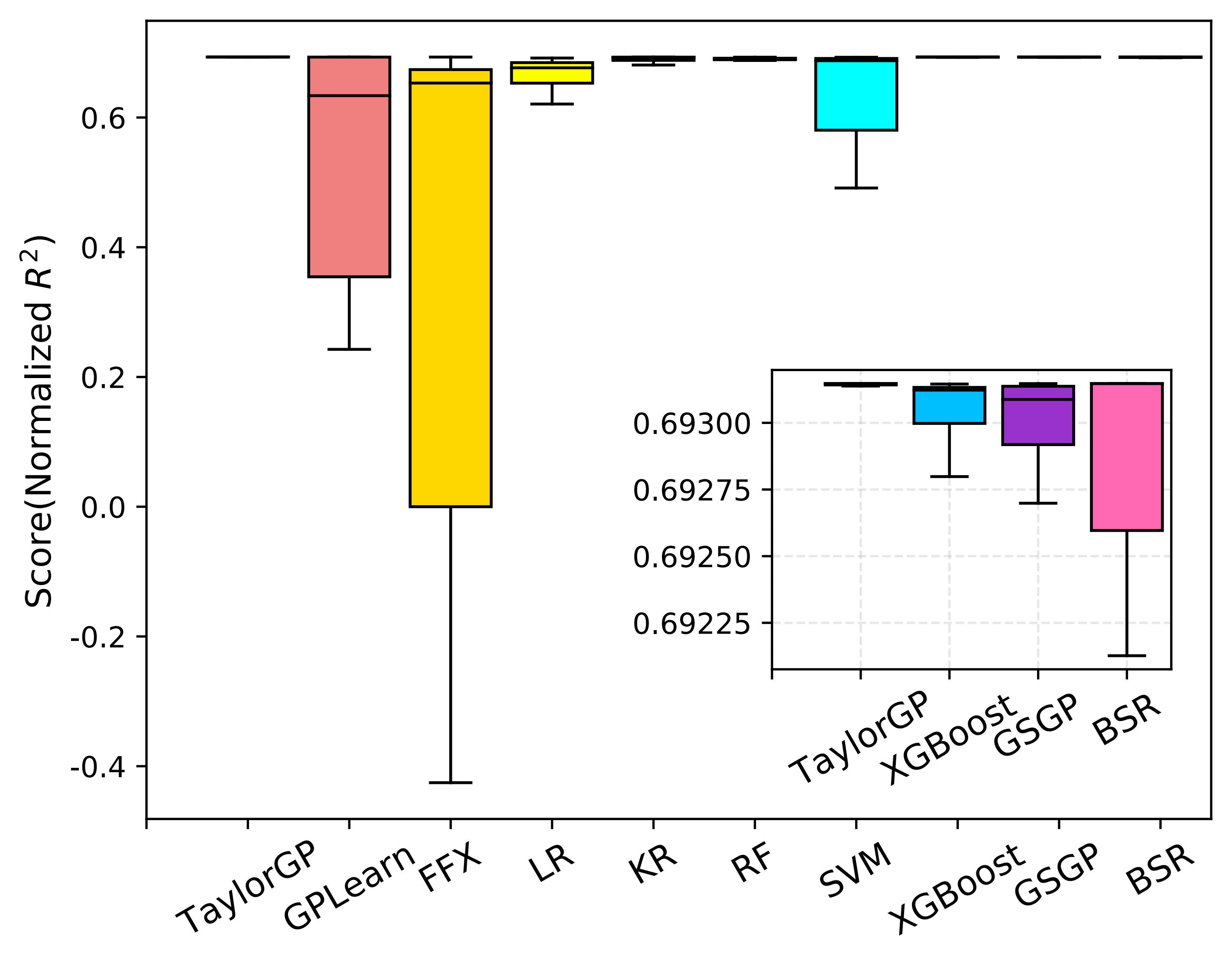
Normalized R^2 comparisons of the ten SR methods on Penn Machine Learning Benchmarks